Dynamic Programming

큰 문제를 작은 문제로 나누어 푸는 문제

vs Divide and Conquer(분할정복)

분할정복은 큰 문제를 해겷하기 어려워서 단지 작은 문제로 나누어 푸는 방법
⇒ 나눈 작은 문제들이 반복되지 않음
DP의 핵심은 작은 부분문제들이 반복

DP 방법

작은 문제들을 한번만 품 ⇒ 정답을 구한 작은 문제들을 메모
⇒ 큰 문제를 풀 때 정답 구한 작은 문제들로 나누어서 메모값 사용

DP 쓸 수 있는 조건

• 작은 문제의 반복
• 같은 문제는 구할 때마다 정답이 같음

Memoization(메모)

한번 계산한 작은 문제를 저장해 놓는 것을 memoization이라고 함

재귀로 푸는 경우

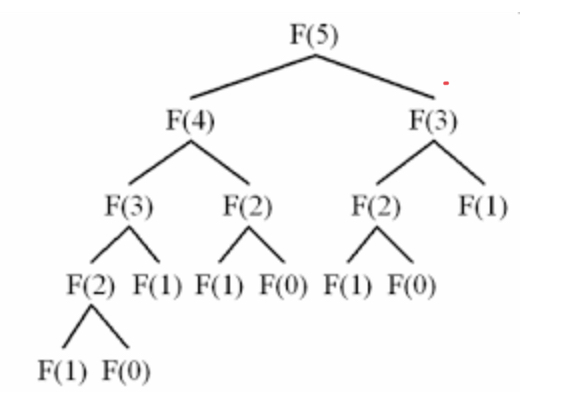
n이 늘어나면 재귀가 기하급수적으로 늘어남
⇒ 시간복잡도 너무커짐

코드

int fibo(int n)
  {
	if (n<=2)
	  return 1;
	else
	  return fibo(n-1) + fibo(n-2);
}

dp를 사용하는 방법

1. 작은 문제들 반복
2. 같은 문제를 구할 때마다 정답이 같음
   위에 그림을 봤을 때 dp의 조건을 만족함
   ⇒ 피보나치를 계산할 때마다, 즉 F(x)의 값을 배열에 저장해놓고 불러오면 되겠다. ( Memoization)

코드

int fiboData[100] = {0,};

int fibo(int n)
{
  if (n<=2) 
	return 1;
  if (fiboData[n]==0)
	fiboData[n] = fibo(n-1) + fibo(n-2);
  return fiboData[n];
}
    ```
보면 재귀의 유무보다도 **memoization** 이 핵심 키워드라고 할 수 있다.
### top-down
> 큰 문제를 방문해서 작은 문제를 호출하는 방식

재귀
```python
int fibonacci(int n) {
    if (n == 0) return 0;
    if (n == 1) return 1;
 
    if (dp[n] != -1) return dp[n];
 
    dp[n] = fibonacci(n - 1) + fibonacci(n - 2);
    return dp[n];
}

bottom-up

작은 문제들부터 답을 구해가며 전체 답을 구해가는 방식

반복

int fibonacci(int n)
{
    dp[0] = 0, dp[1] = 1;
    for (int i = 2; i <= n; i++) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }
}